HALO: Hadamard-Assisted Lower-Precision Optimization for LLMs

[TL;DR] The paper proposes a quantized fine-tuning framework that exploits low bit-width matrix multiplication hardware units by performing quantization online for the inputs, weights, outputs, and their gradients with Hadamard transforms.

Highlights

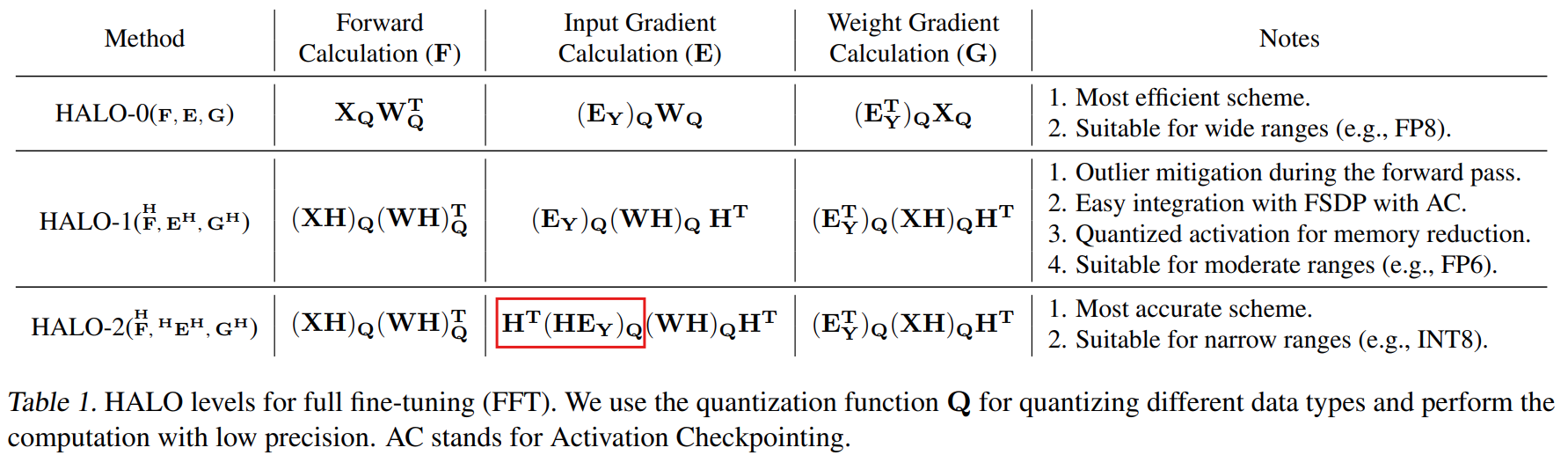
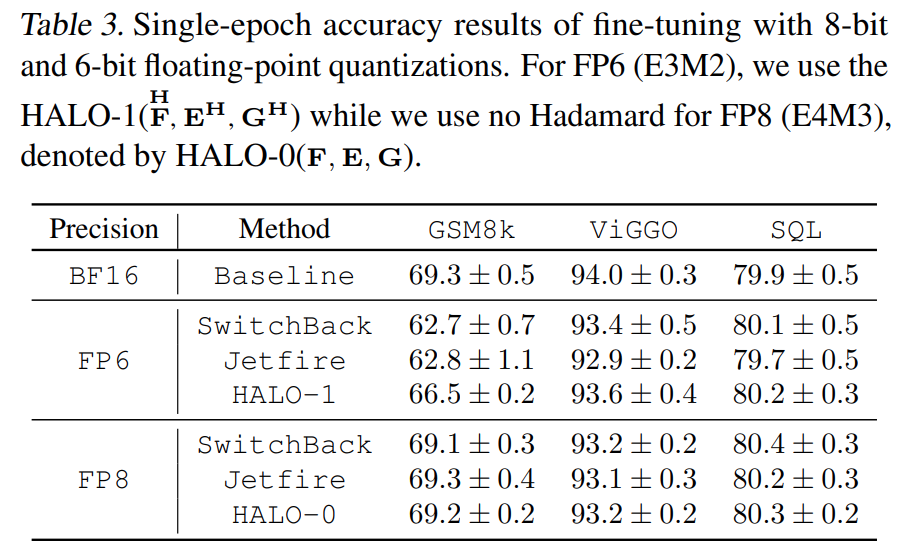
• Provide and experiment with different settings: HALO-0, HALO-1, HALO-2. Speedup: HALO-0 > HALO-1 > HALO-2, Accuracy: HALO-2 > HALO-1 > HALO-0
• Support and experiment with different data types: FP8, INT8, and FP6 for forward and backward passes, exploiting acceleration from low bit-width matrix multiplication hardware units
• Support Fully Sharded Data Parallel (FSDP) scheme to enable further savings by performing low-precision communication
• Support full fine-tuning (FFT) and parameter-efficient fine-tuning (PEFT) methods such as LoRA
• Demonstrate accuracy improvements on downstream tasks for LLAMA-family models in quantized fine-tuning
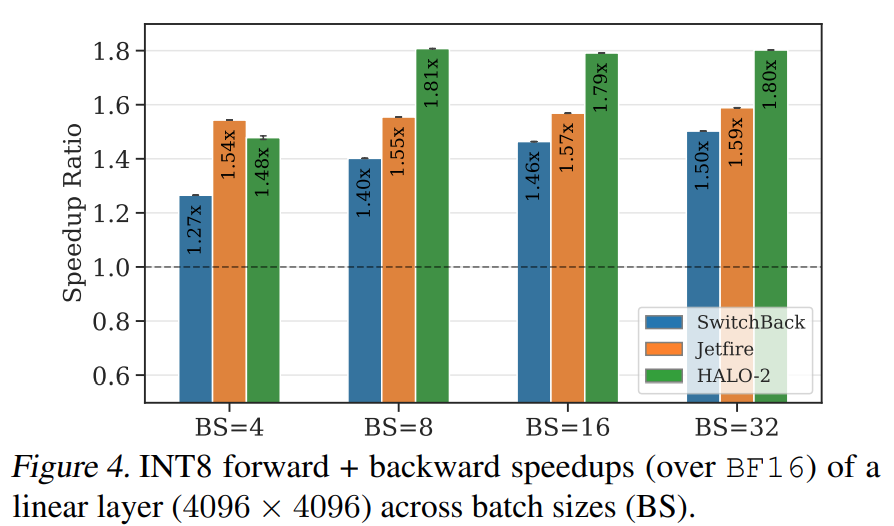
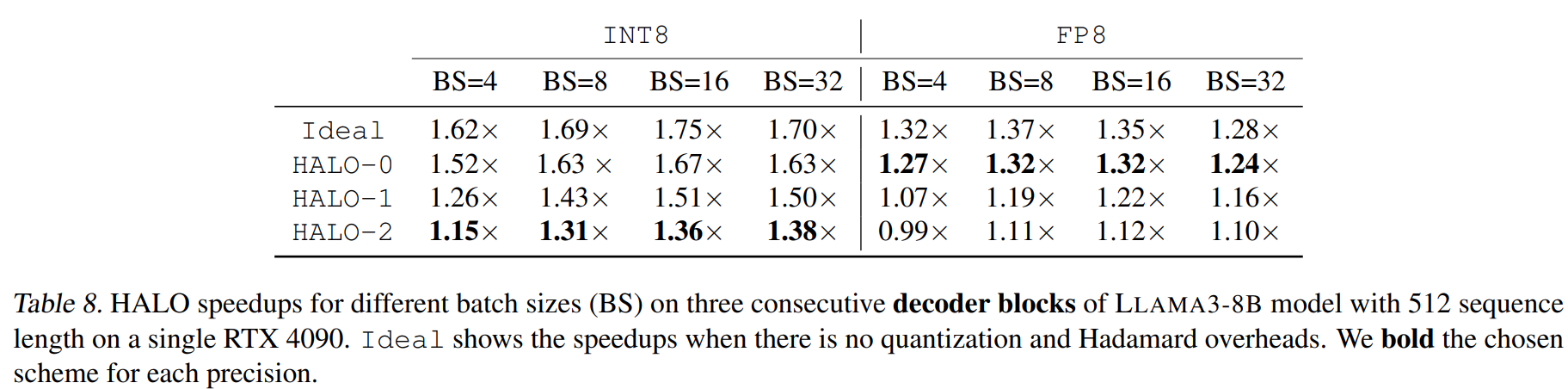
• Demonstrate practical speedups in both FFT and FSDP cases
• Will open-source the kernel implementation at https://github.com/IST-DASLab/HALO

Summary

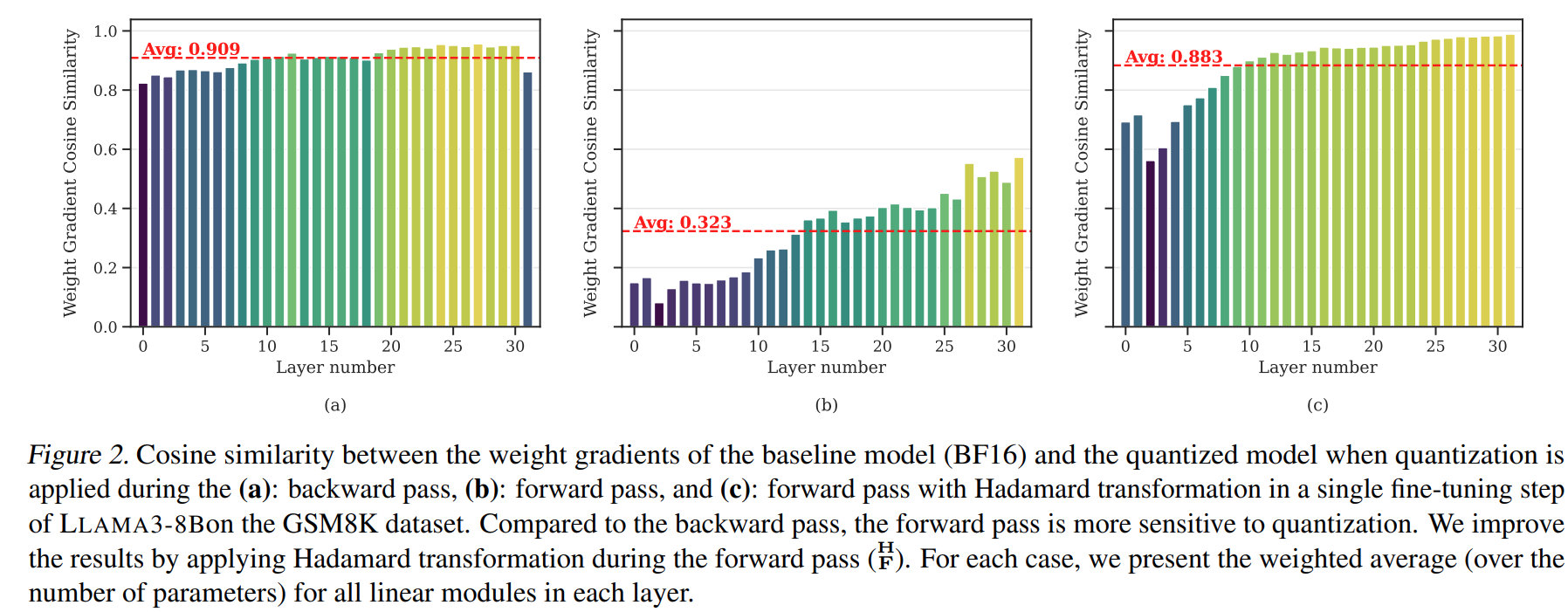
• Observation 1: The quantization errors of the forward activations deviate the gradient direction (compare Figures (b) and (c)).

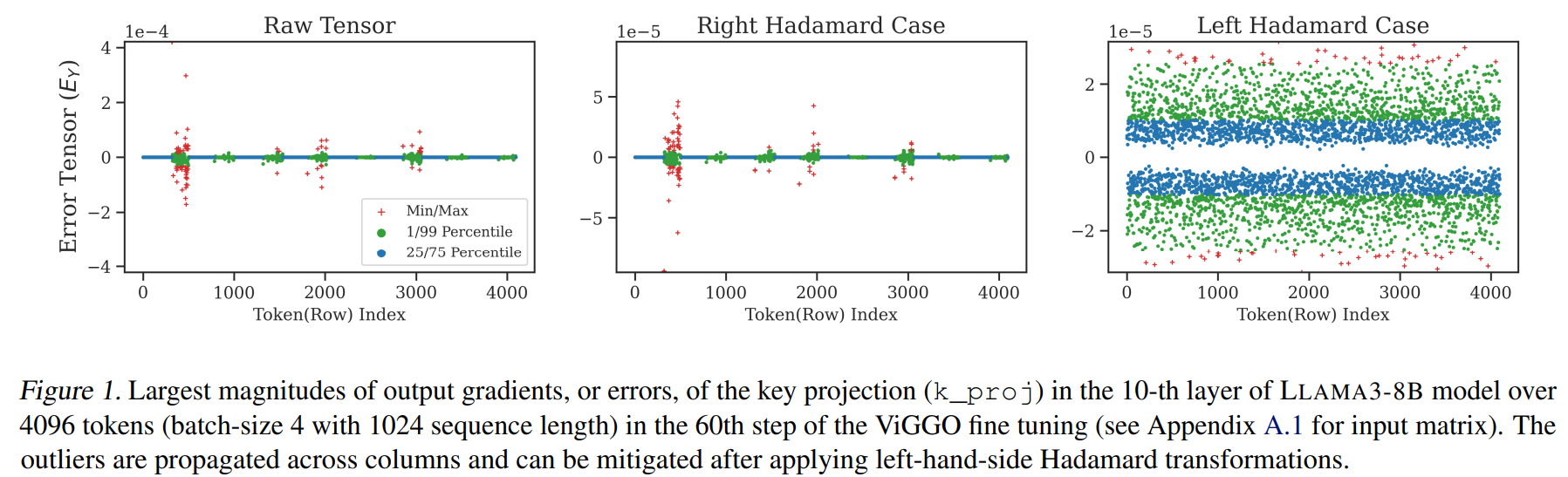
• Observation 2: The outliers of the gradient with respect to the layer output ${\mathbf{E}}_{\mathbf{Y}}$ can only be eliminated by a left-hand Hadamard transformation (see the figure on the right).

• The problem statement: the large outliers in forward activations are difficult to represent in low bit-width data types.
• The solution: The paper addresses this issue by transforming the forward activations online into a smoother space using Hadamard matrices.
• The quantized fine-tuning framework: The proposed method quantizes the transformed inputs, weights, outputs, and their gradients with low bit-width data types (e.g., FP8, INT8, and FP6) in an online fashion to leverage acceleration from low bit-width matrix multiplication hardware units for forward and backward passes.

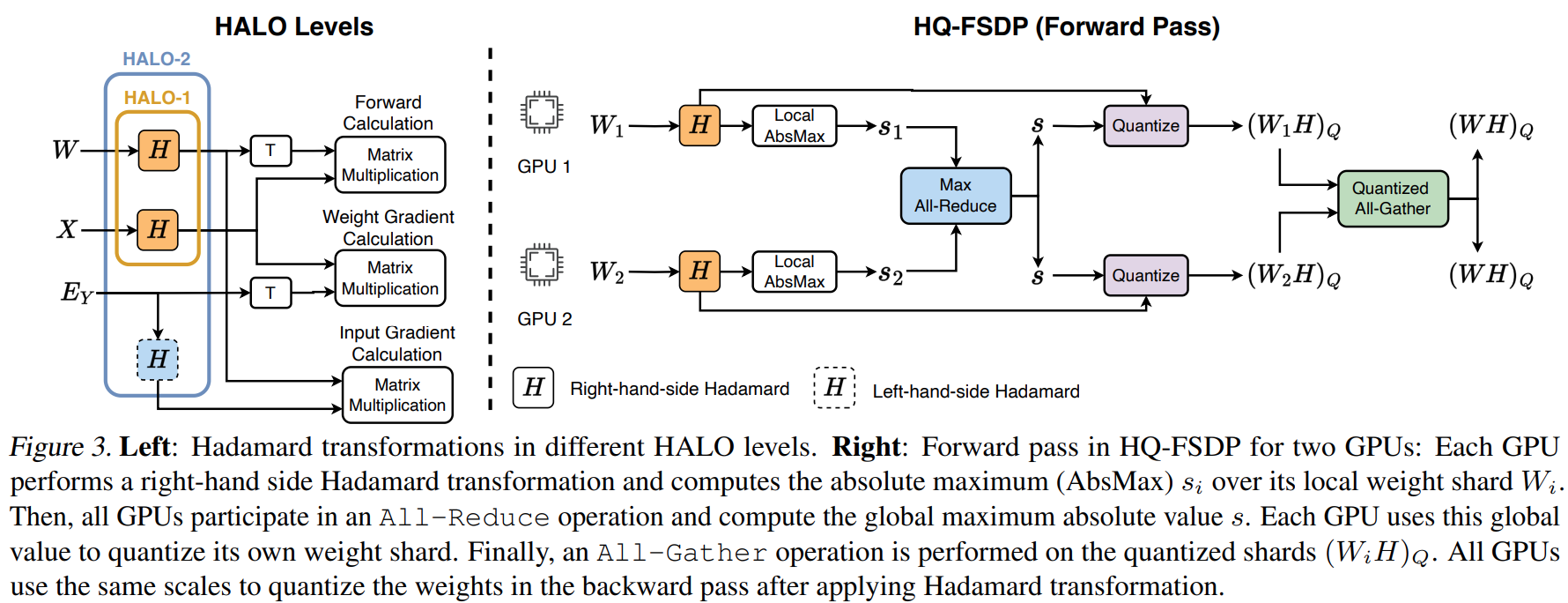
• Different strategies: The paper studies the placement of Hadamard rotations in both forward and backward passes. The left-hand Hadamard transformation (in the red rectangle) is applied to ${\mathbf{E}}_{\mathbf{Y}}$.

Experiments

Compared with Baselines

• Left: Accuracy, Right: Relative speedup

HALO Levels

• Accuracy

• Relative speedup

Notations

The forward and backward passes

• Let matrices $\mathbf{X}\in {\mathbb{R}}^{b\times m}$, $\mathbf{W}\in {\mathbb{R}}^{n\times m}$, and $\mathbf{Y}\in {\mathbb{R}}^{b\times n}$ be the inputs, weights, and outputs with batch size $b$.
• ${\mathbf{E}}_{\mathbf{X}}$, $\mathbf{G}$, and ${\mathbf{E}}_{\mathbf{Y}}$ are the gradients w.r.t. the inputs, weights, and outputs, respectively. The authors also refer ${\mathbf{E}}_{\mathbf{X}}$ and ${\mathbf{E}}_{\mathbf{Y}}$ as errors.
• The forward and backward calculations are defined as $\begin{array}{}\text{(1)}& \mathbf{Y}& =\mathbf{X}\cdot {\mathbf{W}}^{\mathrm{\top }}& \mathbf{\text{(Forward)}}\text{(2)}& \mathbf{G}& ={\mathbf{E}}_{\mathbf{Y}}^{\mathrm{\top }}\cdot \mathbf{X}& \mathbf{\text{(Gradient)}}\text{(3)}& {\mathbf{E}}_{\mathbf{X}}& ={\mathbf{E}}_{\mathbf{Y}}\cdot \mathbf{W}& \mathbf{\text{(Error)}}\end{array}$

Quantization

• Given half-precision (FP16) matrices $\mathbf{A}\in {\mathbb{R}}^{m\times k}$ and $\mathbf{B}\in {\mathbb{R}}^{k\times n}$
• ${\mathbf{A}}_Q$, ${\mathbf{B}}_Q$ are the quantized copies of $\mathbf{A}$ and $\mathbf{B}$.
• Low precision matrix multiplication $\mathbf{Y}={\mathbf{A}}_{\mathbf{Q}}{\mathbf{B}}_{\mathbf{Q}}$

Hadamard Transforms

• No Hadamard Case: $\mathbf{Y}={\mathbf{A}}_{\mathbf{Q}}{\mathbf{B}}_{\mathbf{Q}}$
• Left Case: ${}^{\mathbf{H}}\mathbf{Y}={\mathbf{H}}_{\mathbf{m}}\mathbf{(}{\mathbf{H}}_{\mathbf{m}}^{\mathbf{T}}\mathbf{A}{\mathbf{)}}_{\mathbf{Q}}{\mathbf{B}}_{\mathbf{Q}}$
• Right Case: ${\mathbf{Y}}^{\mathbf{H}}={\mathbf{A}}_{\mathbf{Q}}\mathbf{(}\mathbf{B}{\mathbf{H}}_{\mathbf{n}}{\mathbf{)}}_{\mathbf{Q}}{\mathbf{H}}_{\mathbf{n}}^{\mathbf{T}}$
• Middle Case: $\stackrel{\mathbf{H}}{\mathbf{Y}}=\mathbf{(}{\mathbf{AH}}_{\mathbf{k}}{\mathbf{)}}_{\mathbf{Q}}\mathbf{(}{\mathbf{H}}_{\mathbf{k}}^{\mathbf{TB}}{\mathbf{)}}_{\mathbf{Q}}$