ParetoQ: Scaling Laws in Extremely Low-bit LLM Quantization

[TL;DR]
The paper introduces ParetoQ, a unified framework that compares LLM quantization across 1-bit, 1.58-bit, 2-bit, 3-bit, and 4-bit settings. It discovers a key transition between 2-bit and 3-bit quantization, where models retain their original representations at 3-bit and higher, but undergo substantial changes at lower bit widths. ParetoQ shows that 2-bit quantization is a strong alternative to 4-bit due to its superior efficiency-accuracy trade-offs.

Highlights

• Demonstrates that 2-bit, 3-bit, and ternary quantization often outperform 4-bit in terms of accuracy-memory trade-offs.

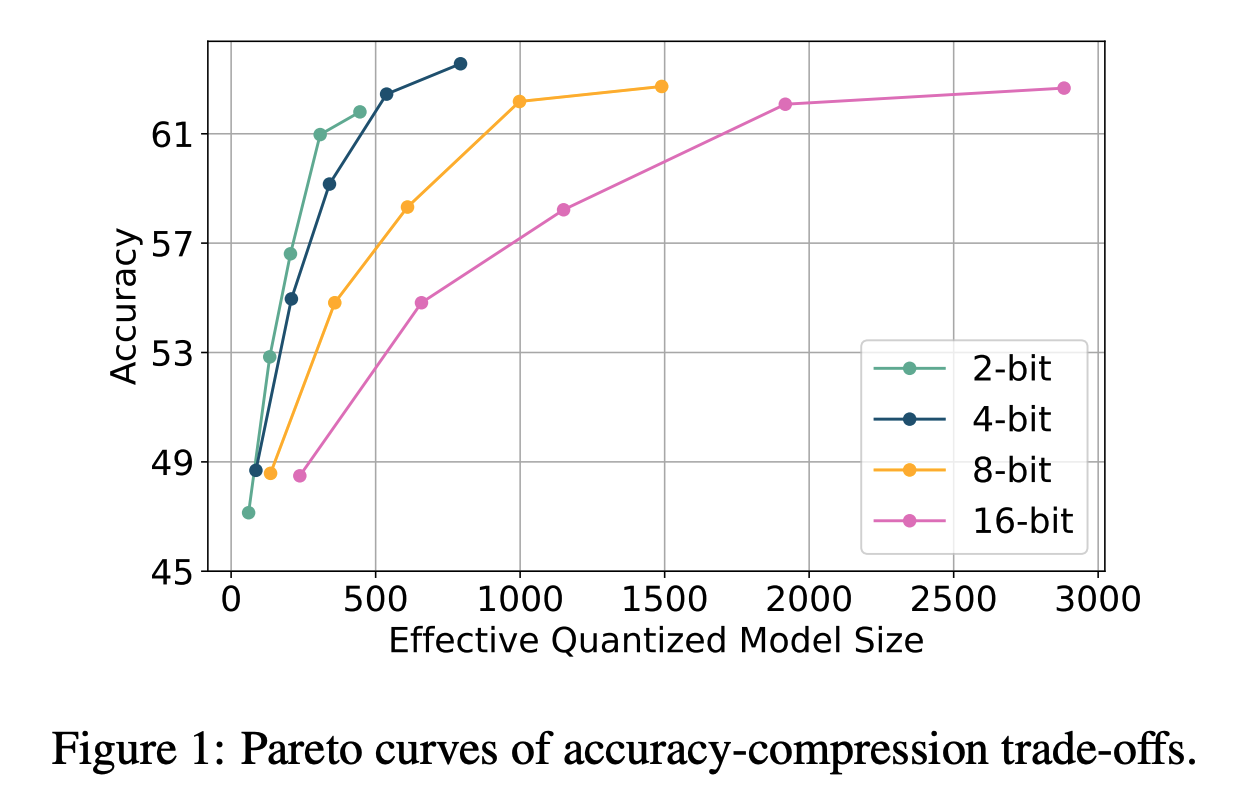
• Identifies a sharp transition between 2-bit and 3-bit quantization, where 3-bit models and above retain pre-trained distributions, while 2-bit models undergo major representation shifts.

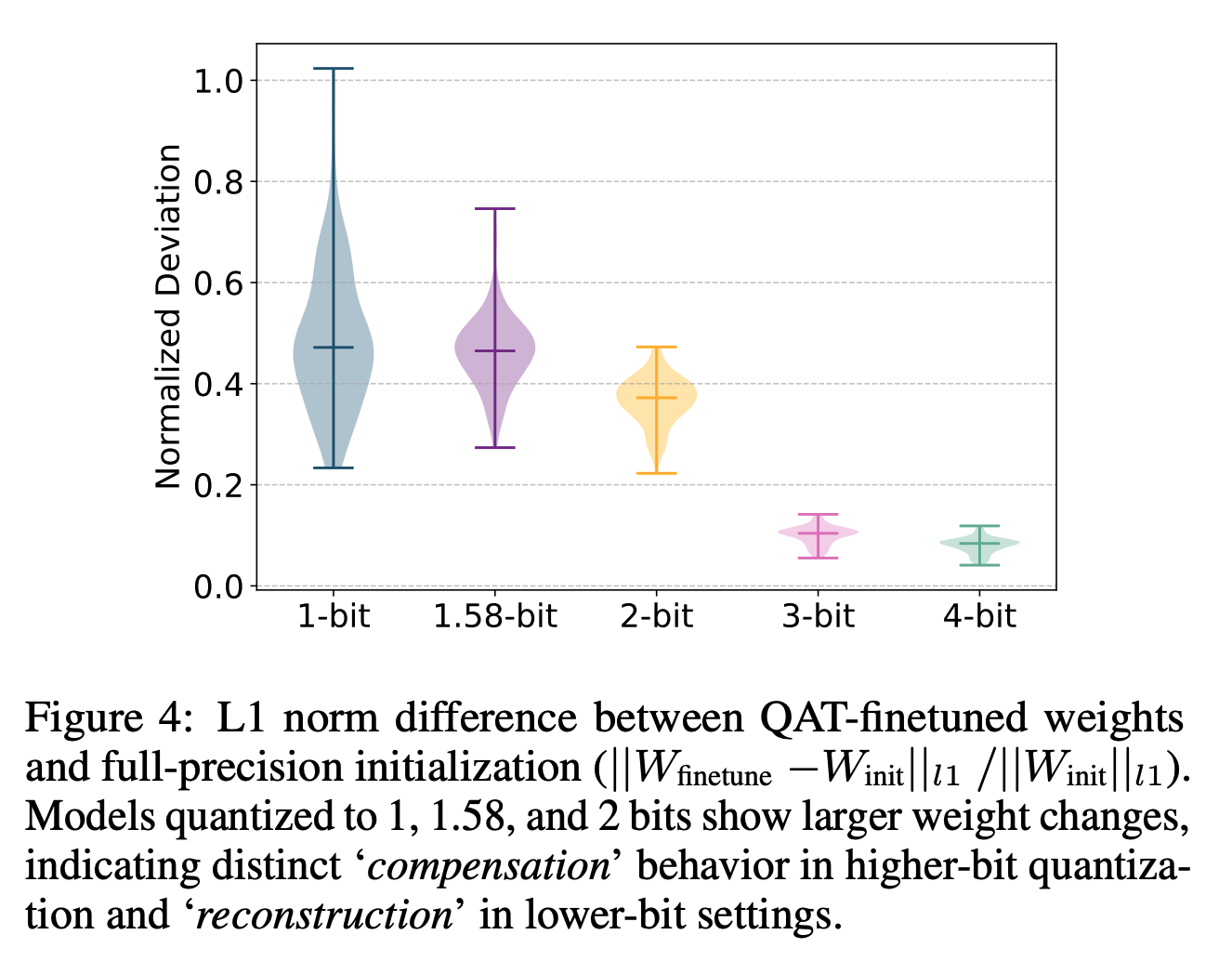
• Quantization-aware training (QAT) consistently surpasses both post-training quantization (PTQ, no fine-tuning) and QAT from scratch.

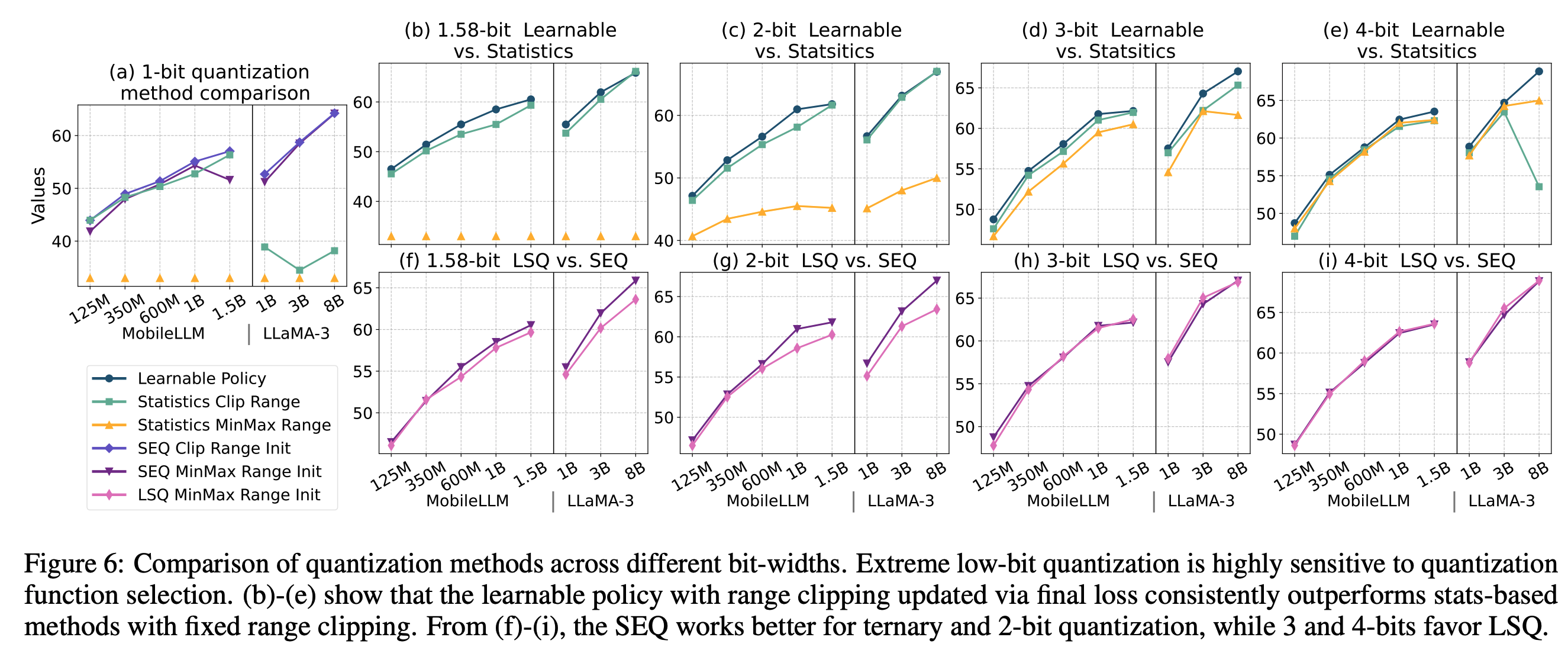
• Propose a refined quantization functions, Stretched Elastic Quant (SEQ), for low-bit settings. ${\mathbf{W}}_Q^i=\alpha (\lfloor \text{Clip}(\frac{{\mathbf{W}}_R^i}{\alpha },-1,1)\times \frac{k}{2}-0.5\rfloor +0.5)/k\times 2$ ${\mathbf{W}}_Q^i=\alpha {\hat{\mathbf{W}}}_Q^i=\{\begin{array}{ll}\alpha \cdot \text{Sign}({\mathbf{W}}_R^i),& \text{if }{N}_{bit}=1\\ \alpha (\lfloor \text{Clip}(\frac{{\mathbf{W}}_R^i}{\alpha },-1,1)\times \frac{k}{2}-0.5\rfloor +0.5)/k\times 2,& \text{if }{N}_{bit}=1.58,2\\ \alpha \lfloor \text{Clip}(\frac{{\mathbf{W}}_R^i}{\alpha },n,p)\rfloor ,& \text{if }{N}_{bit}=3,4\end{array}$

Summary

• Observation 1: Recent studies on scaling laws in the low-precision domain have reached conflicting conclusions.
  • Dettmers & Zettlemoyer and Kumar et al argue that 4-bit or 6-bit quantization often resides on the Pareto frontier, balancing accuracy and efficiency.
  • In contrast, Ma et al. and Kaushal et al. suggest that bit-widths as low as 1.58 bits per parameter offer significant potential for optimal scaling trade-offs.
• Observation 2: Prior studies overlook the impact of the training scheme, denoted as ${\mathbf{S}}_{\text{train}}$, and the bit-specific quantization function $\mathcal{F}$.
• The problem statement: How to determine the optimal trade-off between bit-width and model size while ensuring accuracy?
• The solution: The authors propose a scaling law $\mathcal{L}(\mathcal{N},\mathcal{D},\mathcal{P},{\mathbf{S}}_{\text{train}},\mathcal{F})$ comprising five dimensions, and systematically optimizes quantization functions and training schemes across different bit-widths.
  • Introduces Stretched Elastic Quantization (SEQ), which balances quantization grids for 2-bit and ternary settings.
  • Applies learnable quantization ranges, outperforming static min-max methods.
• The proposed framework: The quantized framework evaluates models under 1-bit, 1.58-bit, 2-bit, 3-bit, and 4-bit precision.

Experiments

• Accuracy-compression and Accuracy-speed Trade-off

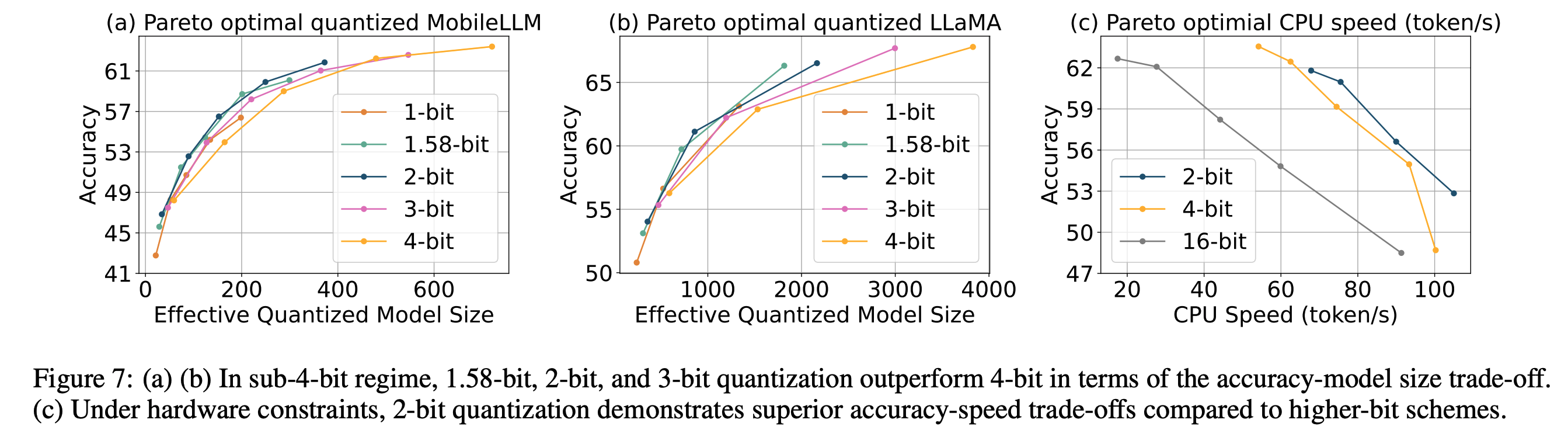
• 2-bit / 3-bit / 4-bit Comparisons

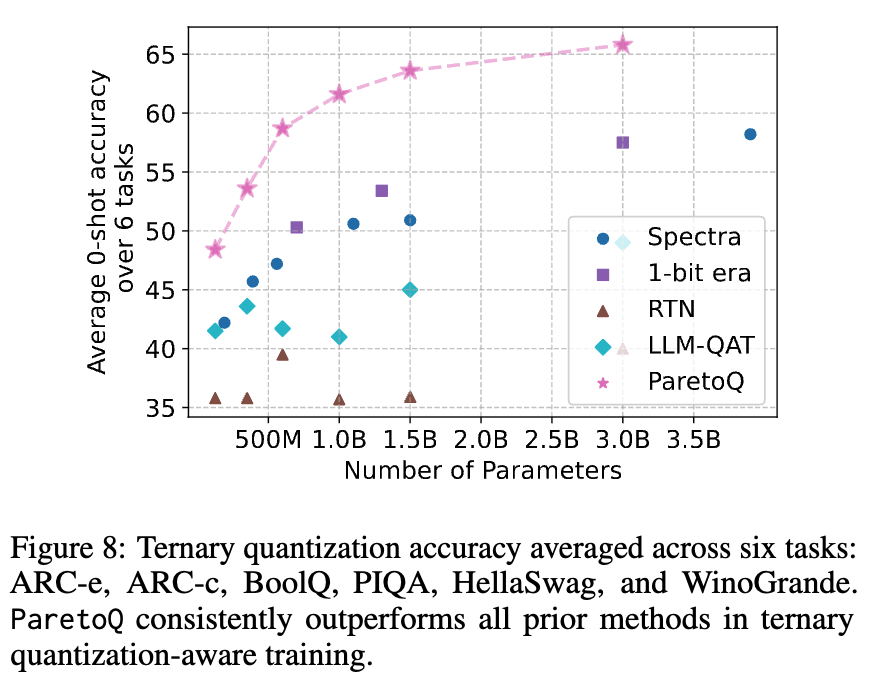
• 1.58-bit Comparison on Sub-8B Models
  • Note: floating-point LLaMA-3 3B model achieves 69.9 accuracy

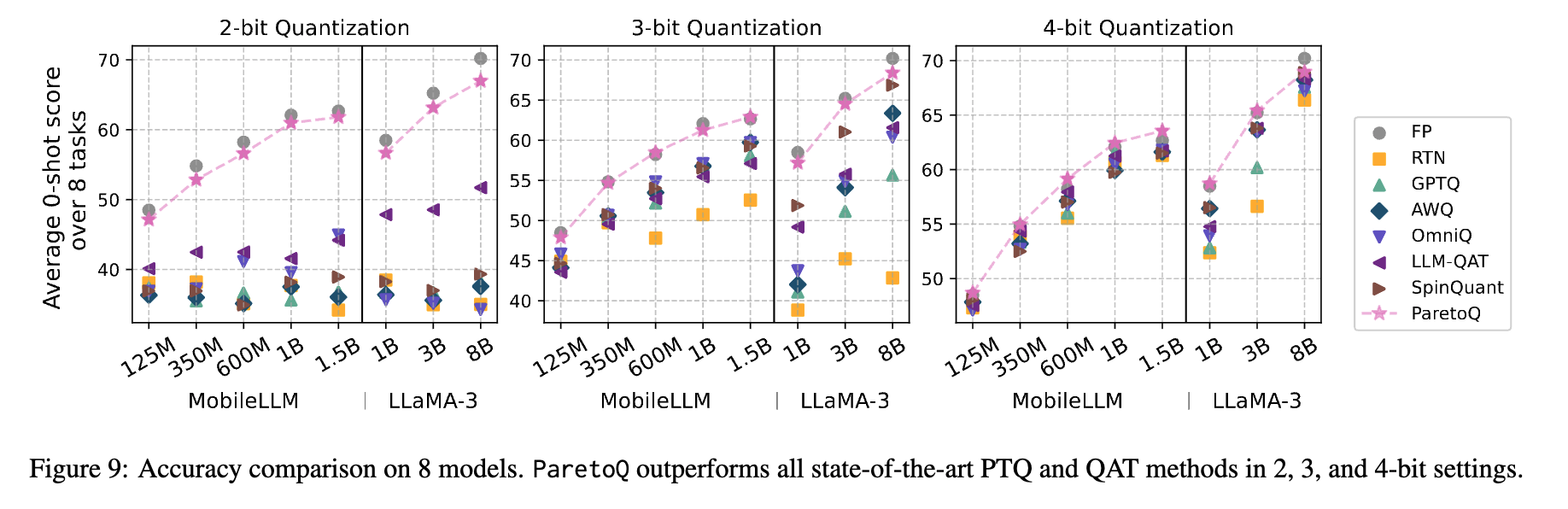
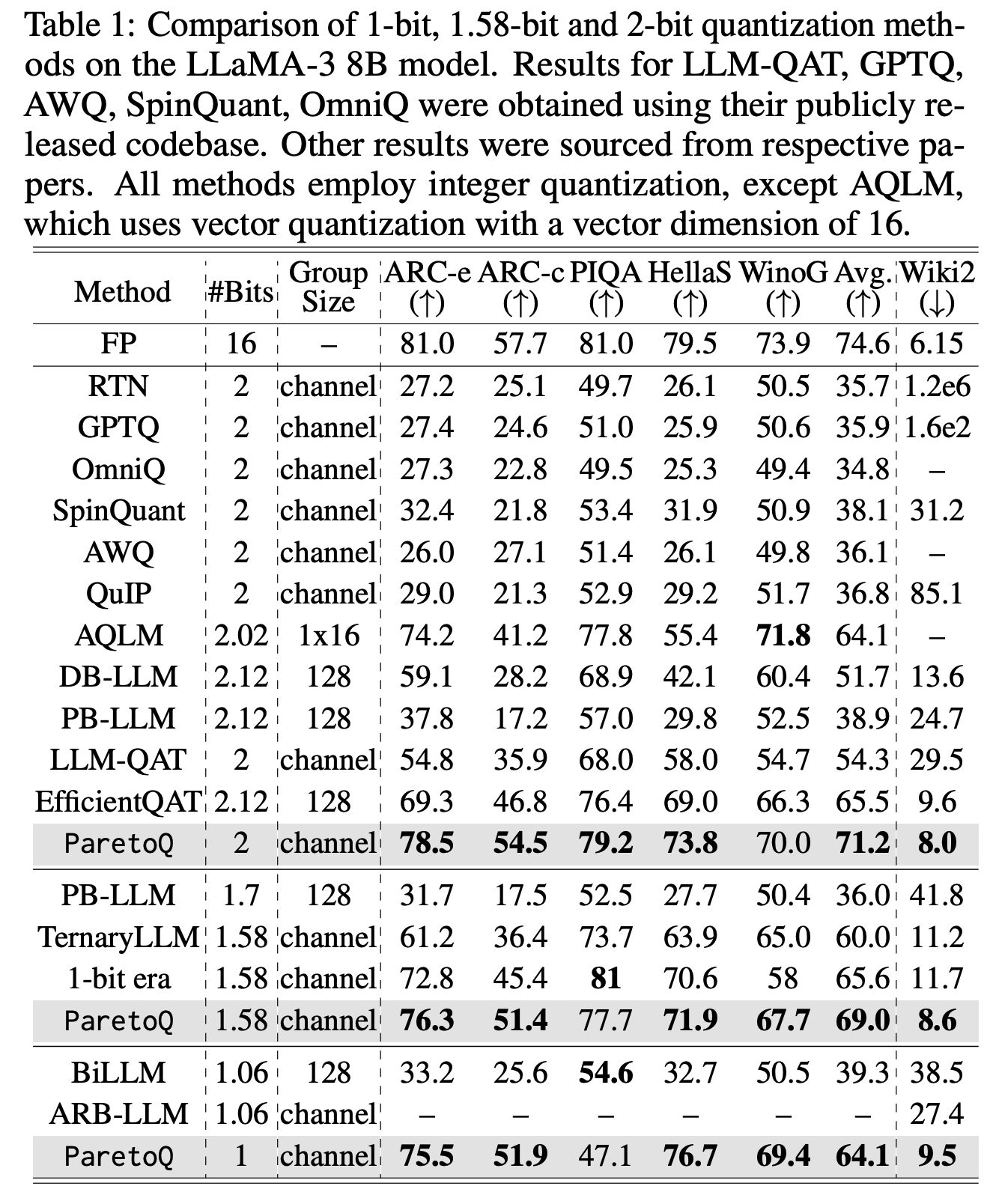
• Main Results

Conclusions

• 2-bit quantization outperforms 4-bit in efficiency-accuracy trade-offs.
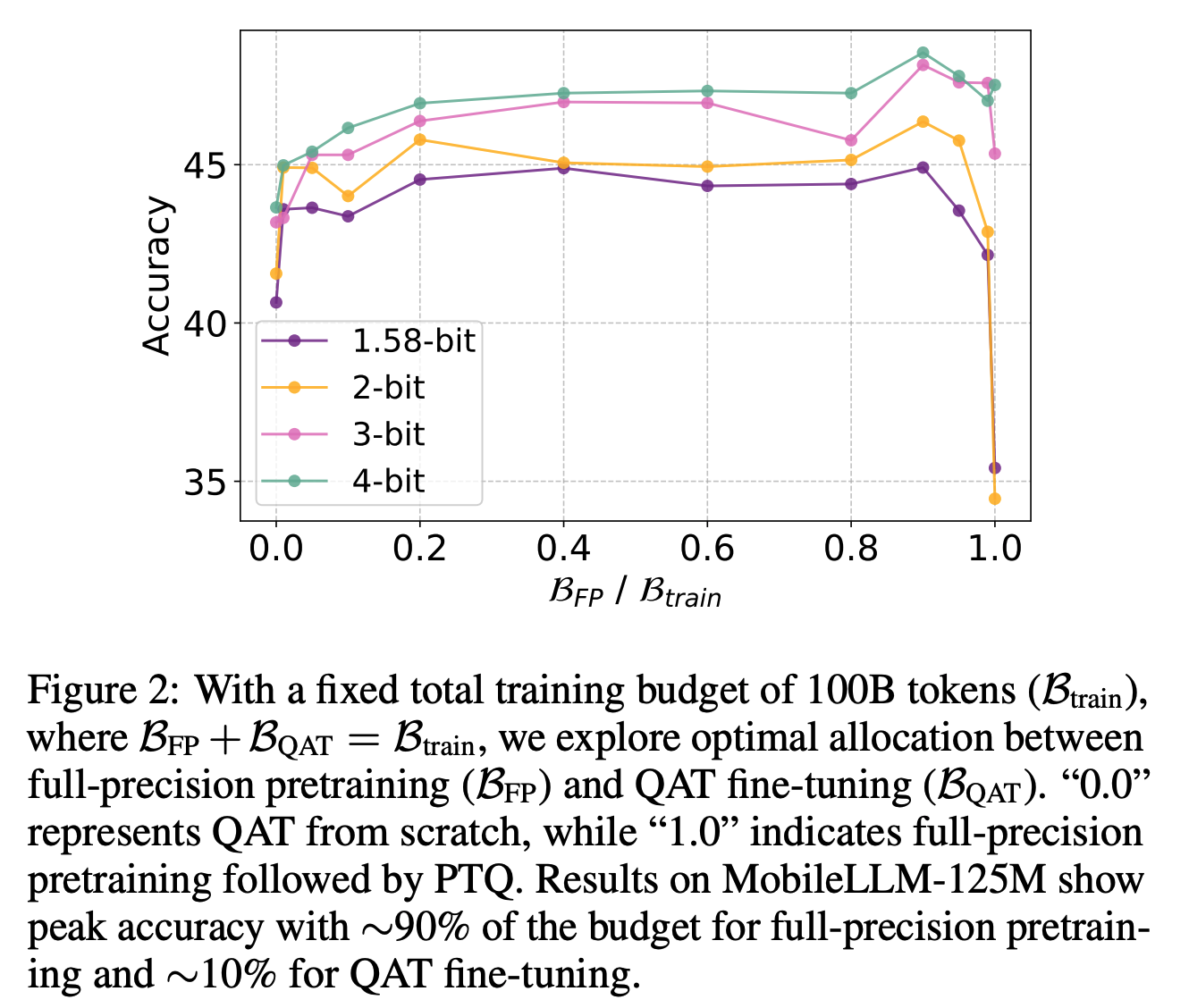
• Fine-tuning is crucial for sub-4-bit quantization, especially for binary and ternary models.
• Quantization-aware training (QAT) finetuning consistently surpasses both post-training quantization (PTQ, no fine-tuning) and QAT from scratch
• QAT serves as a compensation mechanism for bit widths above 2-bit and as a reconstruction process for bit widths below 2-bit, where weights adapt to form new representations.
• Extreme low-bit quantization is highly sensitive to quantization function selection, with no single optimal function for all bit widths.